Understanding the Geometry Formulas on the GED Formula Sheet

Students and teachers are likely very familiar with the formula sheet used for the Math GED exam.  Many have spent hours substituting values in the variables b, l, h, and others.  Many students have found the area of rectangles, triangles, parallelograms, etc., as well as finding the surface area of prisms and pyramids.  But where do these formulas come from? How are they derived? Mark Trushkowsky’s presentation from Summer Institute 2024 explained where many of these formulas come from.

We will start with the most fundamental shape, the rectangle.

For this article, we will assume that we know and understand the formula for area of rectangle: A = length × width.  From here, we can derive the area of a parallelogram, where b is the base, and the h is the height.

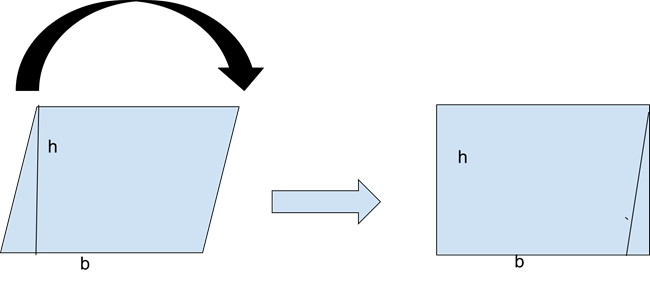
Every parallelogram has a right triangle.  Here we see it on the left side of the parallelogram.  Shift it to the right, and we have a rectangle.  Since we know the area of rectangle is A = length × width, or in this case, b × h, we have the area of a parallelogram is A = b × h.

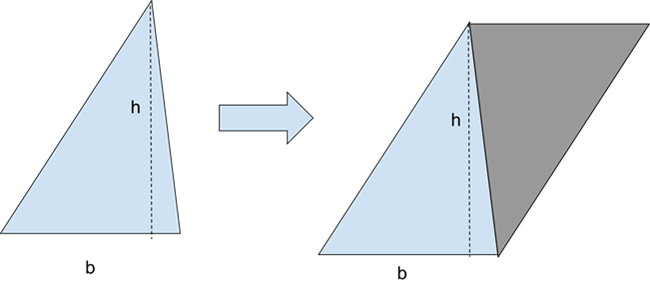
Now that we have the area of a parallelogram, we can derive the formula for the area of a triangle, with base, b, and height, h.  If we take the triangle, rotate it, and “copy and paste” it alongside the original triangle, we see that we create a parallelogram.  We know that the area of the parallelogram is A = b × h.  Since the triangle is one half of this parallelogram, the formula for the area of the triangle is A = ½ b × h.

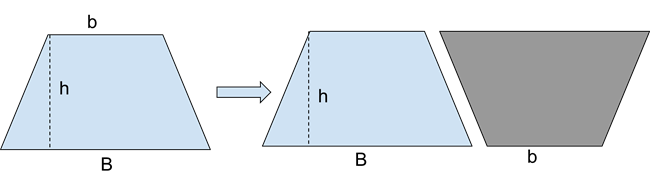
Now let’s move on to the trapezoid, with a height of h, and bases, B and b.  We can see that if we take the trapezoid, rotate it, and then “copy and paste” it to the original trapezoid, we create a parallelogram with base, B + b, and height h. This parallelogram has area A = (B + b) × h.  Since the original trapezoid is ½ of the parallelogram, the area of a trapezoid becomes A = ½ (B + b) × h.

Now that we have derived the formulas for the parallelogram, triangle, and trapezoid, let’s move on to the surface areas for the right rectangular prism. But this time, let’s take a different approach.

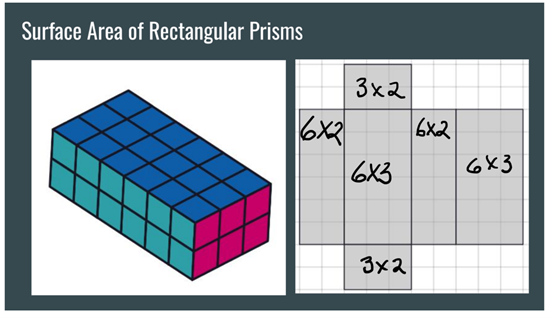
Let’s begin with a right rectangular prism length of 6 units, a height of 2 units, and a width of 3 units.  We will use our understanding of the area of rectangles and our logic skills to find the surface area.  We will then compare this calculation to the general formula for the surface area of a right rectangular prism.

To find the surface area of the prism, it may be useful to unfold the 3-dimensional shape to create the net to the right.  Many people will see many different ways to find the surface area. Some will use the 3-dimensional object and some will use the net.  Here we will use the net.

We can consider the net as 6 rectangles and find the area of each rectangle.  If we note that the rectangles come in pairs, and 3 of the rectangles are doubled, we see that the surface area of the prism is SA = 2 × (6 × 3) + 2 × (6 × 2) + 2 × (3 × 2).  Now let’s recall that the formula for a right rectangular prism is SA = 2 × l × w + 2 × l × h + 2 × w × h.

If we place our calculation above to the formula for surface area, we can see how the formula may be derived.

SA = 2 × (6 × 3) + 2 × (6 × 2) + 2 × (3 × 2)

SA = 2 × l × w + 2 × l × h + 2 × w × h

Not every student will find the area in the same way, but given enough support and opportunity, every student can find a way that works for them.

There are many more formulas for 3-dimensional shapes and surface area. The formulas can be understood in much the same way as the rectangular prism.  The formulas for volume can be understood as well.  For more examples, I encourage you to watch Mark Trushkowsky’s presentation for Summer Institute, 2024:

WATCH: Understanding the Geometry Formulas on the GED Math Formula Sheet >>