Coherence: The Path to the Whole Picture in Math Instruction

Following a 2-part series describing Metro North’s experience making program changes in order to move toward more coherent math instruction, here’s a peek into what I am delving into in my classroom. I hope you feel encouraged and inspired to dive more deeply into this shift of coherence as well!

Addressing the Issue of Coherence in My Classroom

Lately, keeping coherence in mind has been the single most transformative and exciting change I have made to my instruction. I don’t know about you, but it has been disheartening for students to seem to master one skill/concept one week, only to not be able to apply it to a new situation the next week—or even the next day! However, perhaps the solution to the problem is not solely repetition of math facts and problems. Perhaps there is something that we as teachers can tweak in our instructional delivery to help students better solidify their learning.

I found this to be the case for me. I was not really helping students make connections among concepts – both building within and across levels within a domain as well as building across domains. By teaching math more as isolated topics, I was hurting my students. They could not see the bigger picture of mathematical concepts. They were not grasping the fact that “Math” is one picture that resembles neurons with axons and dendrites coming off a cell body, NOT separate folders in a filing cabinet that never share papers. I am now a firm believer that if students cannot see how interrelated math concepts are, they will never be proficient, independent mathematical thinkers!

The Shift

To remedy this and enhance my teaching, I have been trying to create coherence across domains. Specifically, I have been connecting standards in the domain Number and Operations—Fractions with standards in the domain Measurement and Data. In my experience, most every student’s body gets tense or has eyes that roll to the side when the word “fractions” is uttered. Fractions tend to be a nearly universal point of confusion and insecurity. To make matters worse, this is usually what hinders students from making progress in college level courses.

During the last few months in my classroom, we have been covering standards in Numbers and Operations-Fractions in Level B and C (fraction basics + applying operations) in conjunction with a couple standards from Level B and C Measurement and Data (3.MD.8 and 4.MD.3). We first covered the concept of fractions, then moved to multiplying and dividing fractions. Once students had practiced this skill, we then talked about the basics of area, applying that idea to squares and rectangles. Fractions were then brought back into the mix, and multiplying and dividing fractions were applied to area problems.

“What if the object had fractional side lengths? How would we find the area?”

Students were able to review their knowledge of fractions while applying it to the concept of area.

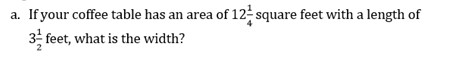
We then moved on to learn/review adding and subtracting fractions. After learning the concept of perimeter, we incorporated adding and subtracting fractions into our lessons on perimeter.

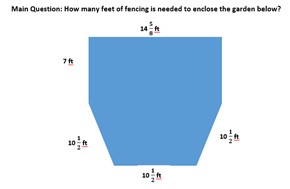
We were even able to sneak in some more measurement practice (more from Measurement and Data) by learning how to measure fractional side lengths with a ruler! Connections!

Even though I am just diving into this more intentional way of teaching, it has been fun to explore ways to achieve coherence in my classroom. I am excited to think about what other connections I can make among standards and domains. Ultimately, it will help my students own their mathematical skills and knowledge.

Achieving Coherence in Our Classrooms

Above is just one example of what can be done with fractions. There are so many different options! I have found that achieving coherence between domains helps keep students engaged in a multi-level classroom. Arguably for most topics, even students who are learning some D and E level standards in a domain will benefit from a review of earlier standards in the content progression. The fact that more basic skills will be used and applied elsewhere affirms the relevancy of the math for higher level students. Be transparent about where you are going with the concepts and skills you are covering. Help students see that math is comprised of interconnected topics that build upon each other. How are they going to see and use this skill later on? For example, not knowing how to efficiently work with fractions will hinder students’ ability to solve for the unknown variable, or use some of the geometric formulas, or be comfortable working with fractional slopes, etc. The main takeaway is that we can specifically build this kind of coherence across domains into any ABE proficiency level. It just takes being intentional about it. (Again, keep in mind that all of what I described above has taken a few months to cover.)

Furthermore, staying on one concept for too long can be boring and frustrating for students. While certainly there is a linear aspect of math, what if we look for ways we can be more circular and “connecting” instead? I find it is more motivating for students to do more math than stay parked in one spot for too long…within reason. Plus, let’s be realistic. As ABE instructors, we don’t have the luxury of teaching linearly, so we need to find ways to cover more ground and make connections more quickly for students. This is one of our superpowers as adult educators!

Check out this resource to help you intentionally build coherence

I recently learned about a new resource that can help you achieve coherence in your classroom. Check out achievethecore.org. Under “Classroom Resources,” click on “Coherence Map.” Below is a screenshot from the coherence map of one of the standards I have been addressing in my instruction: 3.MD.8.

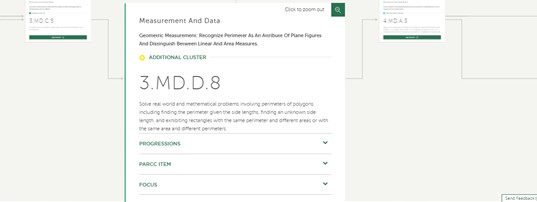
You can see to the left and the right that there are connections drawn between this and other standards. Personally, I could build on what I have done and teach the connecting standards they indicate.

I started this article off by saying that I hope to encourage and inspire you to dive deeper into this shift of coherence for yourself. Some questions I will leave you with to ponder:

1. What connections to other standards can you make to what you are currently teaching in your math classroom?
2. What opportunities can you take advantage of during classroom discussions to explicitly make connections to other math skills and/or content?
3. What’s one step you can take to develop your students’ understanding of math as more of a collection of neurons rather than separate files?