Combatting the Churn: Exploring the Spiral Model of Instruction

The Churn

In our setting, we call it The Churn. It is the weekly revolving door of names and faces on the class roster. Yesterday’s hotshot mathematician has graduated and moved up to the next level of programming, and in his place is a newbie who has not worked a math problem since slide rules were hot technology. Sadly, the newbie was not in class for last week’s hands-on, contextualized, standards-aligned, technology-enriched, confusion-free lesson on determining the lowest common denominator–a lesson that would have made Benjamin Bloom and Madeline Hunter shed tears of exhilarant joy. No, the newbie has no idea of the andragogical brilliance that went into creating that lesson, and, therefore, he knows even less about determining common denominators. What is worse, this week’s lesson on adding fractions is scaffolded on that prior knowledge.

But, what are the options in our battle against the churn? For myself, as a teacher of low-level mathematics, I have often times gotten stuck in the rut of re-teaching the same lesson, over and over, and never moving beyond the Mr. Monotone basics of, “The top number is the numerator, the bottom number is the denominator, and I am the Terminator.” (Though, that particular math joke never gets old.)

In our woeful regurgitation of the same-old, same-old, veteran students grow bored and disinterested; after all, they have seen all of this before and have arrived at the painful conclusion they are “…never going to use this stuff in real life.” It is a disappointment to them that there are never any explorations of real-world applications—no actualizations of overlaying concepts—no a-ha moments to encourage them in their journey. Boredom, ad infinitum. What would you do in their shoes?

Another problem with the churn-induced, rut-concept of Fifty First Dates with a Fraction is that by the time the class actually advances to new operations and challenges, without the mindful feeding of those fledgling fraction neurons, all knowledge of numerators and denominators perishes quickly. Within time, weeks of amazing instruction are seemingly lost. “You never taught us about common denominators.”

“What? I never…?” Slumped shoulders. A deep sigh. Back to Mr. Monotone. “Ok class, the top number is the numerator, the bottom number is the denominator, and I am the Terminator.” (Still chuckle-worthy.)

No! For the sake of those shallow-rooted neurons, we must never again get stuck in the endless rut of re-teaching in that manner. We must liberate ourselves, our students, and our mathematics from that model!

The spiral model

My own fatigue of the churn-rut forced me to search beyond the singularly-scaffolded math models of my youth—you know, one idea per chapter, one chapter every three weeks, quiz-quiz-test-report card—You will definitely need to know how to do this next year in trigonometry. I had to journey beyond those linear explorations. Next week’s new students demanded something of me beyond the status quo. They demanded to experience the breadth of our leveled standards on a consistent basis. They demanded to see the interplay of concepts and to gather for themselves the life-changing tools of critical thinking. Gradually, I felt the promptings toward the spiral model of instruction.

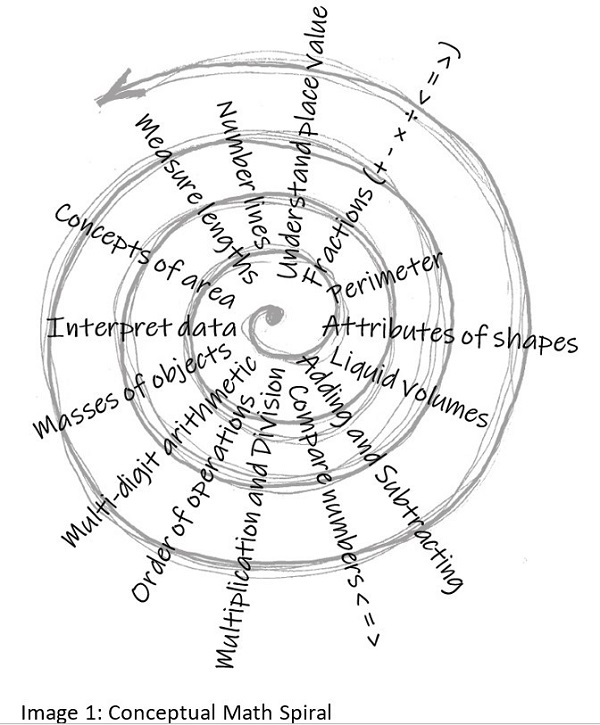In the simplest form of the spiral model, students encounter a wide range of concepts over a short period of time, and they experience these concepts at an increased frequency (Image 1). While a student might not know how to add fractions after their first exposure, they begin to understand that there are such things as fractions and fractions can be added. Likewise, they begin to see the connections to other skills in math in which parts and wholes are dealt with in much the same manner as fractions. After all, math is more than just a menagerie of isolated events and numbers—more than just two trains leaving a station at the same time.

With this internal dawning of a potential move toward the spiral model, but not knowing where to jump in, I asked a colleague, “What if the College and Career Readiness Standards were a curriculum?”

Quite appropriately, the response was, “The standards are only a framework for instruction and learning. They are not a curriculum.”

A framework. That was the answer I needed to hear. The gears began to turn.

Strangely, the word framework caused me to meditate on some old National Geographic recollections of traditional Inuit kayaks—seal-skin stretched across a carefully sculpted wooden frame. In their tectonic design, these kayaks are lightweight, agile, and completely functional in the open sea. In a standards-based, spiral model of instruction, the canvas of daily explorations could be stretched across a carefully sculpted framework of the standards. Students would develop a certain math agility that would empower them to navigate effectively between the operations and to develop deeper connections and understandings.

Implementing the spiral model in class

Lost in the day-dream wanderings of spiral frameworks, I read through my course’s Level A and Level B math standards and created a cursory problem for each standard. The problems were not perfect, nor was that my intent. Those problems served as a stake in the sand for future explorations. A starting point. In fact, my first felt-tip-on-paper iteration of a spiral was quite crude, with only a handful of easily-accessed standards being represented.

When I distributed the materials the next morning, I told my students they were getting the material cold and without any explanations. “Treat this like the TABE test. Answer the questions you know. Mark the ones you do not know. Give an attempt at every question. Show me what you are thinking.”

The students got to work cracking the atom of spiralized-mathematics while I walked among the desks. Peeking over their shoulders, I was surprised to see how much they knew about topics we had never really discussed because we had been stuck in the re-teaching rut of numerators and denominators. Their math was alive and in far better shape than I could have imagined!

After forty-five minutes, when the majority of students were finished, and others were nearly finished, and still others were struggling valiantly, we went over the answers on the board.

I took my time with introducing and explaining each question. Step-by-step we marched. We also discussed how these questions might appear differently in other testing formats, such as the TABE or the GED. These explanations were not a deep drilling into each problem, but rather they were a 10,000 foot overview of the big ideas. Students who got stuck on a problem copied my board work into their notes.  They were encouraged that they were able to get, at least, some of the problems completed and correct. They likewise enjoyed experiencing different math strategies and not, “…fractions again…”

When the class was over, I reminded the students to keep their assignments and notes because they would be seeing similar problems the following week. “These are tools for your mathbox. Take good care of them.” This is the beauty of the spiral model.

The next day, we worked through a few more of the standards, and followed the same post-lesson explanations and discussions. This daily routine continued until we had worked through one problem for each of the standards. The following week, we repeated the whole spiral process. Same standards, different problems. Students were reminded to use the previous week’s materials and explanations as a guide for those new challenges. As they worked, I observed high levels of collaboration between themselves—they were teaching each other! I could hear them attacking each question with confidence. “Remember last week how the teacher said to…” Even the new students contributed a verse to the questions they understood.

Always, our board discussions were replete with questions that helped me to understand the common sticking points (6³≠18). Furthermore, students were invited to share their work and their that-is-not-how-I-did-it methods on the board. We even took time to test the legitimacy of their “shortcuts” to see if they would always work. In our explorations, their ideas were every bit as important as my own.

Seeing how the spiral model proved useful for my students, I was intrigued to explore a little more. Over the course of the following months, I edited the daily problems to something more approachable and created supplemental materials to help students in their areas of struggle. Eventually, my felt-tip originals were replaced by a work smarter, not harder Word.doc that allowed me to print off question stems, write in a new set of numbers, and hit the “Start Copy” button. Each week, I presented new, but familiar, challenges to the students, who were quick to review previous materials before visiting my desk. In time, students developed a robust mathbox of examples and explanations that became crucial allies in those moments of struggle. I was pleased with their strides towards math self-efficacy.

Real-life results

I have dabbled in the spiral model of instruction for a little over a year, and I continue to find that students show steady gains on their TABE tests and they are more confident when they move up to subsequent levels of math instruction. They have a certain joy and pride in the realization that they are learning. “It took me a minute, but now I get it.”

Even after a year, however, my journey into the spiral method of instruction has only scratched the surface of what is possible. My constant editing of material and balancing of standards keeps me busy and forces me to find new ways to re-present old problems. As a result, I am always on the search for connections between what we do in class and real-world applications. After all, we do use this “stuff” in life, every day.

Originally published 7/8/22