- MN ABE Connect
- Archive
- Using Number Categories to Build Coherence – Part 1
 April 24, 2023
April 24, 2023
Using Number Categories to Build Coherence – Part 1
Andy Albee, InstructorHave you ever wondered why we have different number systems? Although many of the students may think so, it is not to confuse students. On March 14 (Pi Day!) I presented a virtual training called Be Rational! Get Real! An Exploration of Number Categories to help explain these different number systems and how they are interconnected.
Understanding how we label numbers and categorize their properties can help us to explain the coherence of operations to our students and connect the CCRS standards.
What are number systems, anyway?
Number systems are ways of categorizing values with common characteristics. The Counting Numbers are our numerical digits 1,2,3,… Whole numbers are these same counting numbers and zero, which cannot be counted, but is not a partial value. Integers are the Whole Numbers and their opposites: -3,-2,-1,0,1,2,3,… Rational numbers are any number that can be written as a ratio of Integers. Irrational numbers are any Real Numbers that cannot be written as a ratio of Integers. Rational and Irrational numbers are discussed more in depth later in these articles.
Starting with whole numbers and place value
First off, our CCRS level A standards discuss working with students in whole numbers 0-20 and using an understanding of place values to help build the concepts of addition and subtraction (1.NBT.2-6). Two important concepts to understand in these early operations are:
1) Numbers can be composed and decomposed.
You don’t have to do a problem with the numbers given; you can change the numbers to be easier to understand and perform the calculations. For example, if we start with:
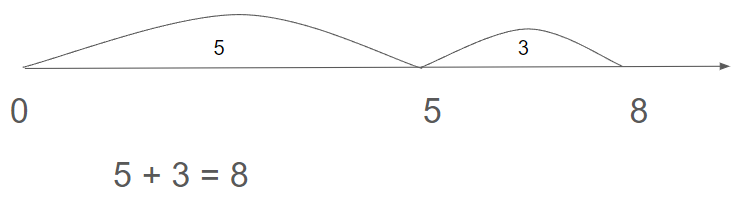
2 + 5 = 7
then we can solve this:
8 + 7 = ?
by decomposing the 7 to make our calculation easier by creating a group of numbers that equals 10:
8 + 7 = 8 + 2 + 5 = 8 + 2 + 5
and then composing the new group of numbers to get the answer:
8 + 2 + 5 = 10 + 5 = 15
2) You can only add “the same stuff to the same stuff and get the same stuff” (the rule of arithmetic closure). This helps us to see that if you add ones to ones, you can only get ones. You can decompose numbers to make the additions easier as shown in the previous problem, but they still add to ones.
Now some of those ones may be exchanged (composed) to tens, but the addition doesn’t do that exchange. The exchange happens after the addition. For example:
25+39 = 20+30+5+9 = 20+30+5+5+4 by decomposing the numbers 20+30 = 50 and 5+9=14.
Then 10 of the ones from the 14 can be exchanged for 1 ten to be added to 50. So 50+14 = 50+10+4 = 50+10+4 = 64.
We can illustrate this on positive whole number lines and show that adding Counting and Whole numbers must result in Counting and Whole numbers.
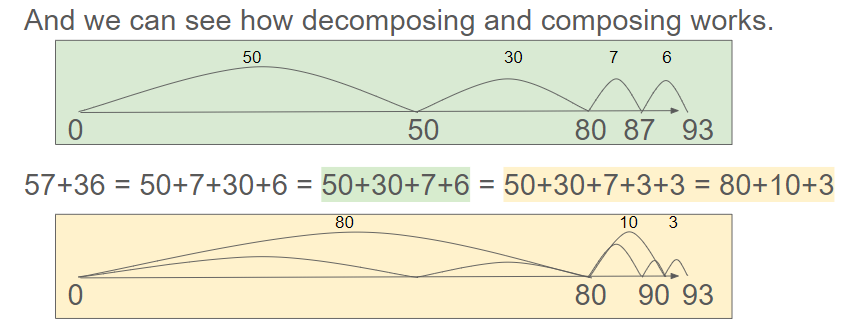
In the problem below, we can see how the addition can be made easier by:
- decomposing 57 and 36 to 50+7 and 30+6
- reordering the values to add numbers with the same pace value; and then
- decomposing 6 into 3+3. We choose to decompose 6 into 3+3 because 7+3 = 10.
When these numbers are decomposed as such, composing the 7+3 from 10 ones into 1 ten that can then be added to the 80 (from the 50+30) makes 57+36 = 80+10+3 = 93.
Many of us may ask why we should look at addition and subtraction this way (I mean, just line up the numbers!). But when we really understand this concept, the operations in other number placement values and categories become easier to understand.
Once students realize this, it can be applied to any part of math:
- Adding in number place value and composing 10s
- Adding fractions with a common denominator and composing 1
- Adding decimals and percentages with common place values and composing 1
- Adding algebraic expressions by combining like terms (sorry, no composing here)
Stay tuned for Part 2!
In our next article on Using Number Categories to Build Coherence, the ideas of how these concepts can be expanded to integers and rational numbers will be explored.

Newsletter Signup
Get MN ABE Connect—the official source for ABE events, activities, and resources!
Sign UpArticle Categories
- ABE Foundations/Staff Onboarding
- ACES/Transitions
- Adult Career Pathways
- Assessment
- CCR Standards
- Citizenship
- COVID-19
- Cultural Competency
- Digital Literacy/Northstar
- Disabilities
- Distance Learning/Education
- ELA
- Equity/Inclusion
- ESL
- HSE/Adult Diploma
- Listening
- Math/Numeracy
- Mental Health
- Minnesota ABE
- One-Room Schoolhouse/Multilevel
- Professional Development
- Program Management
- Reading
- Remote Instruction
- Science
- Social Studies
- Speaking/Conversation
- Support Services
- Teaching Strategies
- Technology
- Uncategorized
- Volunteers/Tutors
- Writing