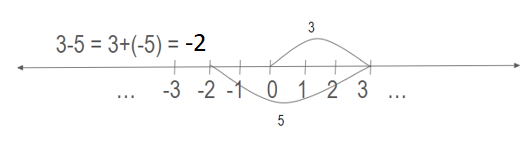- MN ABE Connect
- Archive
- Using Number Categories to Build Coherence – Part 2
 May 19, 2023
May 19, 2023
Using Number Categories to Build Coherence – Part 2
Andy Albee, InstructorIn the previous number categories article, the CCR standards regarding whole number operations were introduced. This article will introduce problems that arose as operations other than addition created numbers that did not fit into the whole number system.
Closed number systems
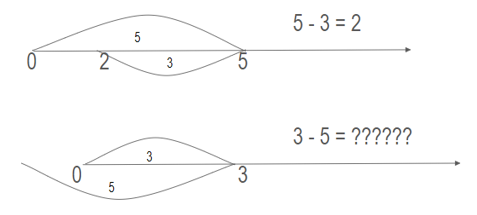
The first problem that we can run into with number systems is that while addition is closed under the whole numbers, subtraction is not. Subtracting a smaller whole number from a larger whole number results in a whole number (whew!), but the closure fails if we subtract a larger number from a smaller number.
Remember: A number category {set} is closed if two elements of it are used in a mathematical operation and result in another element of that set. So whole numbers are closed under addition because adding two whole numbers results in another whole number. Whole numbers are not closed under subtraction as you can subtract a larger whole number from a smaller whole number which does not result in another whole number.
Realizing this, ancient mathematicians added a new category to their whole number system, the integers. Integers are often taught after another category (the rationals), but I like to teach them in relation to the whole numbers to build the number categories in order. Helping students to see how these numbers work on a number line builds the skills to understand how adding and subtracting are related.
The rules for adding and subtracting signed numbers are often confusing to students. However, when students have seen how the whole number operations work, they can build their own understanding of integers. CCR standards involved in the integer category include the standards of 6.NS.5-7.
Subtraction is not necessarily closed based on inner or lower categories, but…
the full integer number line allows us to have a closed system under subtraction:
Note that these concepts continue through addition and subtraction of algebraic expressions. CCR Level E standard A.APR.1 states “Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials.” This is a standard that is often used for the Adult Diploma and is directly coherent with these previous standards.
Like terms in addition/subtraction vs. multiplication
As was shown in the previous article, to add or subtract integers, the values must be in the same decimal number placement. However, you can multiply integer values of different number placements.
In Algebra, we can add or subtract the coefficients of terms that have the same variable part, but we can multiply terms no matter what their variable part is. They do not have to be like terms to multiply the terms. This process follows for algebraic expressions as well.
We do have to add the like terms to get other like terms:
But we can multiply unlike terms and get something different:
So, we can add the 5x2 + (-2)x2, the -3x + x, and the 8 + -7 as they are like terms (have the same variable part).
When we multiply, we can distribute terms that have different variable parts, 9r*6r and 9r*(-4). This results in terms that have different variable parts than when we started: 56r2 – 36r
So building the concepts of the earlier CCRS standards builds the foundation to help us understand Algebra. Often, jumping into Algebra without these earlier standards can cause students confusion and lack of confidence.
In the next article, the standards regarding rational numbers will be introduced.

Newsletter Signup
Get MN ABE Connect—the official source for ABE events, activities, and resources!
Sign UpArticle Categories
- ABE Foundations/Staff Onboarding
- ACES/Transitions
- Adult Career Pathways
- Assessment
- CCR Standards
- Citizenship
- COVID-19
- Cultural Competency
- Digital Literacy/Northstar
- Disabilities
- Distance Learning/Education
- ELA
- Equity/Inclusion
- ESL
- HSE/Adult Diploma
- Listening
- Math/Numeracy
- Mental Health
- Minnesota ABE
- One-Room Schoolhouse/Multilevel
- Professional Development
- Program Management
- Reading
- Remote Instruction
- Science
- Social Studies
- Speaking/Conversation
- Support Services
- Teaching Strategies
- Technology
- Uncategorized
- Volunteers/Tutors
- Writing