Using Number Categories to Build Coherence – Part 3

Multiplication, Division, and Rational Numbers

Multiplication (defined as grouping of sets or repeated addition of factors) is closed under both whole numbers and integers, but division is not.

Helping students to understand that division is the inverse operation to multiplication (meaning we are not grouping but instead breaking into groups or factors) will lead to the understanding that numbers divided by a non-factor will result in a number that is not in the integer category.

For example, if I divide 25 by 2, I will end up with a number that is not in the integer category (in this case, 12.5). I divided 25 by a number that is not one of its factors. Now we build the rationals (introduced in CCR standards 3.NF.1-3, 3.OA.1-7).

Rational numbers are any number that can be written as p/q where p and q are integers (example: 25/2). The CCR standards 4.NF.1-5 build this system with understanding how fraction operations work. Again, true understanding of whole-number system operations is the foundation for operations with fractions (only adding the same number placements relates to only adding fractions with common denominators). Fractions can be composed and decomposed exactly as whole numbers can be to make operations easier to perform. If students can see fractions as just another number and that all the properties of integers apply to them as well, fractions become less scary.

Operations with Fractions… Oh My!

For many of us, the reason for only adding fractions with common denominators is because it’s “just a rule”, rather than a natural progression from earlier concepts. Because of this, the rules for multiplication and division seem even more confusing. Showing students how these operations work can help them to see the “why” behind the rules.

Adding and subtracting rationals is easy…

when the denominators are the same: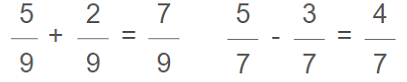

and composition/decomposition works as well: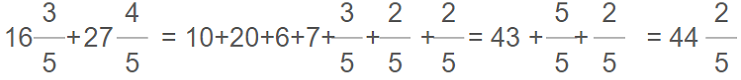

including multiplying by 1; multiplying with a ratio where the numerator and denominator are the same makes an equivalent ratio: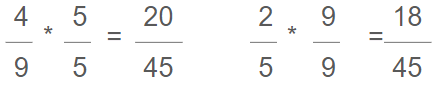

So, now we can add Rationals with different denominators!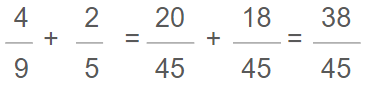

The most confusing part of rational numbers is commonly the division of fractions by fractions. If we understand the process of fraction multiplication (multiply the numerators and denominators), then we can work with the direction of dividing the same way. Unfortunately, these divisions can give us a fraction of a fraction. Through simplifying these fractions of fractions by multiplying by versions of one, the rule of “flip the second fraction and multiplying” emerges!

But how we do divide rationals confuses some students. If we remind them that they are just rationals and divide the same way we multiply, then the algorithm makes sense.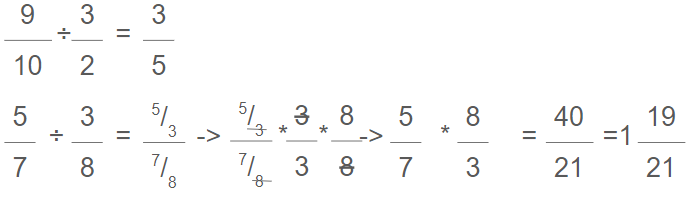

The other part of rational numbers is that they can be written as decimals by restricting the denominators to the powers of 10, and as percents by restricting the denominator to 100. When students see these numbers as forms of rational numbers, they can build the operations with the decimals and percents. CCRS expands to decimals and percents in standards 4.NF.6-7, 5.NF.1-2, and 6.RP.3.

Rational numbers are where most students believe we stop and that rational numbers are the last of the subset categories. However, our final article of this set will investigate the last of the number categories involved in the CCRS, the irrationals.