- MN ABE Connect
- Archive
- Using Number Categories to Build Coherence – Part 4
 June 23, 2023
June 23, 2023
Using Number Categories to Build Coherence – Part 4
Andy Albee, InstructorIn the previous articles on number categories (see Part 1, Part 2, and Part 3), the number systems of whole numbers through rational numbers have been discussed. This article, the last of the series, introduces the irrational numbers and imaginary numbers.
By creating numerical categories from whole to rational numbers, the four mathematical operations – addition, subtraction, multiplication, and division – are closed.
Wait – did we just break math?
 When the Greeks (and other cultures) recognized the operations of exponents and roots, they thought they still had everything covered. As the Pythagoreans believed, “The Gods write the universe in rational numbers.” It was known that the sum of the squares of the legs of a right triangle was equal to the square of the hypotenuse (the Pythagorean Relationship a2+b2=c2). So it looks like math is still closed!
When the Greeks (and other cultures) recognized the operations of exponents and roots, they thought they still had everything covered. As the Pythagoreans believed, “The Gods write the universe in rational numbers.” It was known that the sum of the squares of the legs of a right triangle was equal to the square of the hypotenuse (the Pythagorean Relationship a2+b2=c2). So it looks like math is still closed!
However, Hippasus, one of the Pythagoreans, wrote a proof showing that if the triangle had legs of 1, then the hypotenuse would equal √2 and this number cannot be rational. The rest of the Pythagoreans were so upset by this that they built a grave stone to symbolize that Hippasus was dead to them! They thought that math was broken.
The proof that shook the Greek world
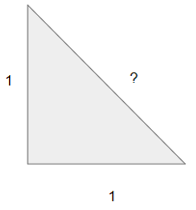 The Greeks (and many other cultures) already understood that for a right triangle, the sum of the square of the legs was equal to the square of the hypotenuse: a2+b2=c2. But what if the legs were both equal to 1?
The Greeks (and many other cultures) already understood that for a right triangle, the sum of the square of the legs was equal to the square of the hypotenuse: a2+b2=c2. But what if the legs were both equal to 1?
By the well-known (by mathematicians) relationship a2+b2=c2, we get 12+12 = 1 + 1 = 2 = c2. Therefore c = √2.
Now, the proof that √2 is incommensurable shook them so much that they cast out Hippasus as dead!
Assume that √2 = a/b where a and b are mutually prime. Then b√2 = a.
Squaring both sides we get 2b2 = a2. Therefore a is even, as it has a factor of 2.
For a and b to be mutually prime, b must be odd (or else we could reduce a/b).
We can then write that as a = 2p (an even number) and b = 2q-1 (an odd number), with p and q as integers.
Then 2b2 = a2 can be written as 2(2q-1)2 = (2p)2 or 2(4q2 – 4q + 1) = 4p2.
Dividing the last equation by 2 results in 4q2 – 4q + 1 (an odd number) = 2p2 (an even number). Contradiction!
Irrational and real numbers
But math was not in fact broken; by creating another math category (the irrational numbers) that does not have a subset of the other categories, the issue was corrected! Furthermore, to make it all work, mathematicians created yet another category (the real numbers), which includes all the rational and irrational numbers. The CCRS (College & Career Readiness Standards for Adult Education) discusses the irrational numbers in standard 8.NS.2.
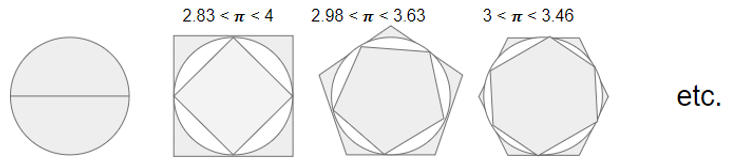
In addition to √2, another main irrational number that we use often is 𝛑 (pi). Since it was believed that all numbers had to be rational, mathematicians spent decades trying to rationalize 𝛑. Some tried to “square” the circle too. It took one Dutch mathematician, Ludolph van Ceulen, 25 years to compute 𝛑 to 35 accurate places by using a polygon with 262 sides (that’s 4,611,686,018,427,387,904 sides). He was so proud that he had the number engraved on his gravestone.
Now, with the invention of Calculus and computers, we can prove that 𝛑 is irrational and we can find the value of 𝛑 to over 31.4 trillion places! While that is interesting, it is not particularly useful. According to NASA’s Jet Propulsion Laboratory, calculating the circumference of the known universe using 𝛑 to 38 places will give us a value with a maximum error of the size of a hydrogen atom. In fact NASA only used an approximation of 𝛑 to 6 decimal places to send humans to the moon!
The important part of the concept of 𝛑 is that it is just a number. Many students and teachers give 𝛑 a reverence more than it deserves. Note that 𝛑 is approximately 3.14 (according to the GED Formula sheet), 3.141592654 (on most calculators) or 22/7 as an approximated fraction. Any of these values work fine for problems most students will face, but 𝛑 ≈ 3 will also work as an approximation for many questions with an error of only 4.5%. Most multiple choice questions (that many of the equivalency tests use extensively) can be answered within this amount of error. Helping students see this approximation can gain them points on the tests and confidence in their problem-solving skills.
While the CCRS does not have any standards regarding imaginary or complex numbers, it can be nice to let students know that there is a math operation that cannot be closed. Taking the square root of a negative number creates a value that cannot be connected to any of our number systems. Also, creating a fraction with a denominator of zero creates an expression that is undefined or indefinite. It’s okay that these issues arise and cannot be fixed or closed. Math is not broken even though these issues cannot be connected.
The big takeaway on number categories
Here we are at the conclusion of this four-part series. So what is the “big idea”?
The CCRS is organized by building concepts of numerical categories. It is incredibly beneficial for students to understand the coherence of these concepts from levels A to E to make all the concepts of operations easier. Taking the time to lay the foundation in whole numbers and build coherently from there will create the space needed for understanding of the subsequent concepts to naturally follow and flow.

Newsletter Signup
Get MN ABE Connect—the official source for ABE events, activities, and resources!
Sign UpArticle Categories
- ABE Foundations/Staff Onboarding
- ACES/Transitions
- Adult Career Pathways
- Assessment
- CCR Standards
- Citizenship
- COVID-19
- Cultural Competency
- Digital Literacy/Northstar
- Disabilities
- Distance Learning/Education
- ELA
- Equity/Inclusion
- ESL
- HSE/Adult Diploma
- Listening
- Math/Numeracy
- Mental Health
- Minnesota ABE
- One-Room Schoolhouse/Multilevel
- Professional Development
- Program Management
- Reading
- Remote Instruction
- Science
- Social Studies
- Speaking/Conversation
- Support Services
- Teaching Strategies
- Technology
- Uncategorized
- Volunteers/Tutors
- Writing